- ホーム
- 蒸気のお役立ち情報
- もっと知りたい蒸気のお話
- 伝熱 後編(円筒の場合)
蒸気の基本
伝熱 後編(円筒の場合)
円筒の伝熱
「伝熱 前編(平板の場合)」では、伝熱の基礎として、蒸気から被加熱物への平板を介した伝熱について解説しましたが、今回は円筒の場合の伝熱について説明致します。
熱交換器のチューブや蒸気輸送管のような円筒では、熱は円筒の内面から外面に向かって(またはその逆向きに)半径方向へ放射状に移動しますが、平面の時のように熱通過を考えれば、円筒の伝熱も同様に取り扱うことが出来ます。
但し、管の場合、径が決まれば総面積は長さに比例するので、単位面積当たりとするより、単位長さ当たりの放熱量(=放熱面積込み)として表した方が便利です。
単位長さ当たりの放熱面積を算出するために、式の中に直径が入ります。
この時、配管の厚みや保温層の厚みなどがありますので、どの位置を各層の直径とするかによって、面積が異なります。そのため、厚みによって外径と内径の算術平均を用いたり、対数平均を用いたりします。
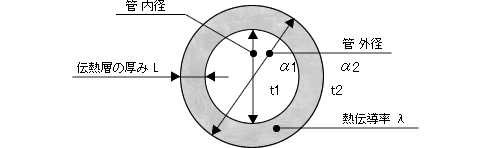
熱伝導(伝熱抵抗)
平板の際と同様に伝熱抵抗(熱の伝わりやすさの逆数)を考えます。
熱の伝わりにくさは伝熱抵抗と考えることができ、熱伝導率と伝熱面積に反比例し、厚みに比例します。
平板の際は R=(1/λ)×L の形になりますが、
これは円筒の場合も同じです。円筒の場合、伝熱面積は直径が決まれば、あとは長さに比例するため単位長さ当たりの面積(Sa)をあらかじめ分母にかけておきます。
| R1 | =(1/λ)×L×(1/Sa) =(1/λ)×L×(1/(π×(内径+外径)/2)) |
省エネルギーセンターの資料によると、管や保温層の厚みが外径の20%以上ある場合は、算術平均よりも対数平均で直径を表した方が正確だそうです。
その場合の式は次のようになります。
| R1 | =(1/λ)×L×(1/(π(外径-内径)/ln(外径/内径)) |
※ln:自然対数
蒸気との熱伝達
蒸気から管の熱伝達や管(保温外壁面)から大気への熱伝達も平板の時と同様に熱伝達率αで考えますが、これも熱伝導と同様、円筒の場合は単位長さ当たりで表します。蒸気から管への熱伝達率をα1、管から大気への熱伝達率をα2、管の内面積をSb、外面積をScとすると、
| R2 | =(1/α1)×(1/Sb) =(1/α1)×(1/(π×管内径) |
| R3 | =(1/α2)×(1/Sc) =(1/α2)×(1/(π×管外径)) |
全伝熱抵抗Rは
R=R1+R2+R3
伝熱抵抗の逆数が熱の伝わりやすさですので、熱通過率JをJ=1/Rとすると単位長さ当たりの熱量は下式のようになります。
Q=J×(t1-t2)
ある長さの配管全体を考える場合は長さLpをかけて、
Q=J×(t1-t2)×Lp
平板の場合の
Q=U×(t1-t4)×A
と似た形で表すことが出来ます。